Em meados de 1687 Isaac Newton apresentou ao mundo uma espécie de tratado sobre o movimento – “Philosophiæ Naturalis Principia Mathematica”. No núcleo de tudo se encontravam as três leis que não podem ser derivadas de princípios mais fundamentais e tudo que se move o faz de acordo com elas. É dispensável comentar a importância dos trabalhos de Newton para a compreensão da natureza. Ocorreu que esses trabalhos foram estudados e explorados até que surgiu uma nova maneira de enxergar o movimento.
Por volta de 1788 uma reformulação da mecânica foi organizada e apresentada por Joseph-Louis Lagrange no “Mécanique Analytique”, dando origem ao chamado formalismo lagrangiano. Vale adiantar que apesar do nome, Jean-Baptiste D’Alembert e Leonhard Euler foram tão importantes quanto Lagrange no desenvolvimento da nova interpretação da mecânica.
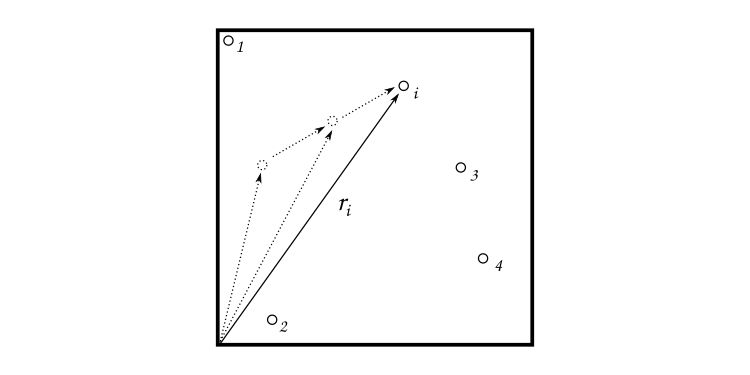
Imagine que há caixa com $N$ partículas idênticas e que o movimento de uma delas está sendo analisado.
Como todas são idênticas, não faz diferença se a análise é feita sobre a partícula $1$ ou sobre a partícula $2$. Então pode-se falar que a análise do movimento é feita sobre a $i$-ésima partícula.

A segunda lei de Newton, quando reescrita na forma
\[\textbf{F}_i = \frac{d \textbf{p}_i}{dt} = m\frac{d \textbf{v}_i}{dt} = m \textbf{a}_i \label{eqa}\]sintetiza a ideia de que a variação na velocidade de uma partícula $ i$ é proporcional a uma força externa aplicada a ela.
A ideia de trabalho relaciona essa força externa $F_i$ à distância $dr$ percorrida pela partícula enquanto estiver sob efeito da força, através de
\[W = \int F_i \cdot \textbf{dr}\]Historicamente a noção de trabalho realizado por uma força esteve presente no estudo da estática, através do princípio do trabalho virtual. A ideia é que um sistema composto por $N$ partículas em equilíbrio estático, sujeito a forças externas $\textbf{F}_{i}^{e}$, poderia se mover para diferentes direções $\delta \textbf{r}_i$ – respeitando as restrições impostas pelos “vínculos de movimento”, que são os elementos que não fazem parte do sistema, mas que de alguma forma interferem em seu movimento. Por exemplo: uma corrente deslizando pela borda de uma mesa; ao adotar a corrente como sistema, há um vínculo com a mesa que limita seu movimento.
Pelo Princípio do Trabalho Virtual a condição de equilíbrio é aquela em que o trabalho das forças externas em todas as direções possíveis soma zero, ou seja
\[\delta W = \sum_{i} \textbf{F}_{i}^{e} \cdot \delta \textbf{r}_i = 0\]Antes de prosseguir, para aliviar a notação, vou abandonar a representação de vetores como caracteres em negrito, adicionalmente passo a adotar a seguinte convenção para escrever derivadas no tempo:
\[\frac{df}{dt} \equiv \dot{f} \nonumber\]Finalmente, o que D’Alembert fez em “Traite de Dynamique” foi usar a ideia do trabalho virtual, típica de problemas de estática, para tentar resolver problemas de dinâmica. Ele fez isso da seguinte forma:
De $\ref{eqa}$
\[F_i = \dot{p}_i \\ \Rightarrow F_i - \dot{p}_i = 0 \nonumber\]Então
\[\sum_{i} (F_i - \dot{p}_i) \cdot \delta r_i = 0\]uma vez que o termo dentro dos parênteses é zero.
Segundo as leis de Newton a variação de momento é devido a forças resultantes, portanto $F_i$ pode ser decomposta em forças externas $ F_{i}^{e}$ e forças de vínculo $f_{i}$. Então
\[\begin{aligned} \sum_{i} [(F_{i}^{e} + f_{i}) - \dot{p}_i] \cdot \delta r_i = 0 \\ \sum_{i} (F_{i}^{e} - \dot{p}_i) \cdot \delta r_i + \sum_{i} (f_i - \dot{p}_i) \cdot \delta r_i = 0 \end{aligned}\]Ao restringir o interesse a sistemas onde as forças de vínculo são nulas – por exemplo: sistema Terra-Sol –, chega-se ao Princípio de D’Alembert
\[\boxed{ \sum_{i} (F_{i}^{e} - \dot{p}_i) \cdot \delta r_i = 0 } \label{eqb}\]Não raro os livros-textos usam a $\ref{eqb}$ para a obtenção de resultados mais interessantes do ponto de vista operacional. Contudo, é interessante ver como Princípio de D’Alembert pode ser usado em um problema de estática.
Como exemplo, considere um sistema de duas massas, conectadas por um fio inextensível e de massa desprezível, ambas sobre meio-cilindro, conforme ilustrado no diagrama a seguir
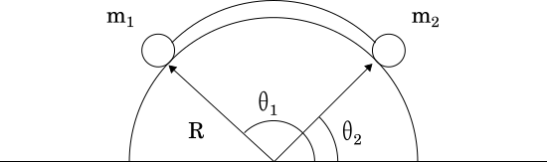
Surge uma boa oportunidade de retomar a ideia de vínculo: considerando que as massas compõem o sistema, há um vínculo entre o sistema e o meio-cilindro.
Imagine que a figura é uma fotografia do sistema no instante $t=t_0$. Se o meio-cilindro não existisse, o movimento do sistema nos $t>t_0$ seguintes seria vertical – ele cairia, certo? Mas como há a metade de cilindro lá, nos próximos $t>t_0$ o sistema é obrigado a descrever uma espécie de movimento circular, em torno do centro do meio-cilindro de raio $R$. Na prática o vínculo impõe restrições ao movimento do sistema.
Alguém poderia questionar a palavra “restrição”, já que no exemplo o sistema se moveria apenas na vertical sem o vínculo, e com ele o movimento se dá em ambas as direções, vertical e horizontal – ou seja, pensando no sentido usual da palavra “restrição”, o movimento sem o vínculo parece ser mais restrito, por ser limitado a uma direção apenas.
Nesse sentido, vale a pena entender a ideia de restrição apenas como uma imposição a qual o movimento do sistema está sujeito. É instrutivo, portanto, pensar que quando há um vínculo, há uma dependência – no caso do exemplo, entre os deslocamentos horizontal e vertical. Em outras palavras: o deslocamento horizontal do sistema em torno da superfície do meio-cilindro é uma função do quanto o sistema se deslocou na vertical – e vice-versa.
Tudo isso observado, resta tentar descobrir qual é a condição de equilíbrio. Segue de $\ref{eqb}$ que
\[\begin{aligned} \delta W &= \sum_{i} \left[ F_i - m_i \ddot{r_i}\right] \cdot \delta r_i & = 0 \\ &= \left[ F_1 - m_1 \ddot{r_1}]\cdot \delta r_1 + [F_2 - m_2 \ddot{r_2}\right] \cdot \delta r_2 &= 0 \end{aligned}\]como, em coordenadas esféricas, a posição $s$ de um ponto na superfície do cilindro é função de um ângulo $\theta$, de modo que
\[s=R\theta \\ \Rightarrow \ddot{s}=R\ddot{\theta} \nonumber\]e, em particular para as posições das massas $m_1$ e $m_2$, o deslocamento angular de uma implica no deslocamento angular de outra, ou seja
\[\ddot{\theta}_1=\ddot{\theta}_2 \nonumber\]segue que
\[\begin{aligned} &= \left[ -m_1 g - m_1 R\ddot{\theta}]\cdot \delta r_1 + [-m_2 g - m_2 R\ddot{\theta}\right] \cdot \delta r_2 = 0 \end{aligned}\]Esses $ \delta r_i$ são deslocamentos virtuais e por definição podem apontar para qualquer direção. Nesse exemplo o sistema pode se mover em duas direções, vertical e horizontal, que vou chamar de $y$ e $x$, respectivamente. Conforme comentado anteriormente, os deslocamentos nessas direções dependem um do outro, então para a analisar o equilíbrio basta ver o que acontece com uma delas. Escolhendo $y$
\[\begin{aligned} y_i &= Rsin\theta_i \\ \Rightarrow \delta y_i &= R cos\theta_i \delta \theta_i \nonumber \end{aligned}\]não perdendo de vista que, devido ao vínculo entre as duas massas, $ \delta \theta_1 = \delta \theta_2$, segue que
\[\begin{aligned} &= -m_1 g \cdot \delta y_1 + m_2 g \cdot \delta y_2 - (m_1 cos\theta_1 + m_2 cos\theta_2) R\ddot{\theta} R \cdot \delta \theta = 0\\ &= -m_1 g R cos\theta_1 \cdot \delta \theta - m_2 g R cos\theta_2 \cdot \delta \theta - (m_1 cos\theta_1 + m_2 cos\theta_2) R\ddot{\theta} R \cdot \delta\theta = 0 \end{aligned}\]como no equilíbrio a aceleração é nula
\[\ddot{\theta}=0 \nonumber\]chega-se em
\[\begin{aligned} \delta W = [ -m_1 g R cos\theta_1 - m_2 g R cos\theta_2 ] \cdot \delta \theta = 0 \end{aligned}\]que tem a mesma forma da $\ref{eqb}$. Para que a igualdade seja válida sempre é necessário que
\[\boxed{\frac{P_1}{P_2} = -\frac{cos\theta_2}{cos\theta_1}} \nonumber\]que é a condição de equilíbrio do sistema.
Vale a seguinte observação: embora $\delta\theta=0$ também satisfaça a condição de equilíbrio, deslocamentos nulos impossibilitam o uso da definição de trabalho virtual.
@book{9780201657029,
Author = {Herbert Goldstein and Charles P. Poole Jr. and John L. Safko},
Title = {Classical Mechanics (3rd Edition)},
Publisher = {Pearson},
Year = {2001},
ISBN = {9780201657029},
URL = {https://www.amazon.com/Classical-Mechanics-3rd-Herbert-Goldstein/dp/0201657023}
}